안녕하세요! 길동이 사촌형입니다 ;)
오늘은 선호체계에 대해 알아봅시닷
이번 시간은 쉬어가는 타임~
😏
1. 선호관계의 의미
길동이에게 A와 B 중에 무얼 더 선호하냐고 물어봅시다.
길동이는 무조건 셋 중 하나로 대답할 것입니다.
- A가 더 좋아
- B가 더 좋아
- 똑같이 좋아
A가 B보다 더 좋은 경우에는 아래와 같이 표기합니다

이 경우는 A를 B보다 '명백하게 더 선호(strictly prefer)'하는 것으로,
강한 선호라고 부릅니다.
A와 B 사이에 아무런 차이를 느끼지 못한다면
A ~ B
와 같이 물결 기호를 사용하여 표기합니다.
A가 B보다 더 좋거나 같다고 느끼는 경우에는 아래와 같이 표기합니다

선호 기호와 물결 기호를 합쳐놓았죠
이 경우는 A가 최소한 B만큼 좋다고 느끼는 것으로,
약한 선호라고 부릅니다.
이러한 관계를 통칭해서 '선호관계'라고 합니다.
2. 선호체계의 공리
앞으로 선호체계를 수치화해서 효용함수라는 개념을 도입할 것입니다.
선호체계를 효용함수로 나타내기 위해서는 몇 가지 전제 조건이 필요합니다.
소비자이론의 기저를 이루는 선호체계의 공리들을 알아봅시다
2-1. 완비성 (completeness)
모든 가능한 상품묶음의 짝에 대하여 선호관계를 설정할 수 있다는 가정
간단히 말하면, 길동이에게 A와 B 중에 뭐가 더 좋냐고 물어봤을 때
길동이는 A가 더 좋다거나, B가 더 좋다거나, 둘 사이에 차이를 못 느낀다는 등의 선호관계를 설정할 수 있다는 것입니다
'글쎄 뭐가 더 좋은지 모르겠어~'는 허용이 안 된다는 거죠.
2-2. 이행성 (transitivity)
소비자의 선호에 일관성이 있다는 뜻
예를 들어서 길동이에게 A와 B 중에 무엇이 더 좋냐고 질문하자 A를 골랐다고 가정합시다
B와 C 중에는 B가 더 좋다고 골랐다면,
일관성에 의해서, 자연스레 A와 C 중에서는 A가 더 좋다는 것을 내포하게 됩니다.
A가 B보다 좋고, B가 C보다 좋지만, A보다는 C가 좋다는 비일관적인 상황은 배제한다는 가정입니다.
2-3. 연속성 (continuity)
상품묶음에 포함되어 있는 상품의 양이 아주 작은 폭으로 변화해 갈 때 선호관계가 점진적으로 변화할 것을 요구함을 의미
말이 쉽게 와닿지 않을 수 있는데요,
그래서 이해하기 편하도록 반례를 들고 왔습니다.
사전편찬법식 선호순서가 연속성을 위배하는 대표적인 사례입니다
사전편찬법식 선호에서는 두 상품묶음의 선호관계를 비교할 때 특정 상품 하나의 양을 우선적으로 비교하고 난 다음에 나머지 한 상품을 따지게 됩니다
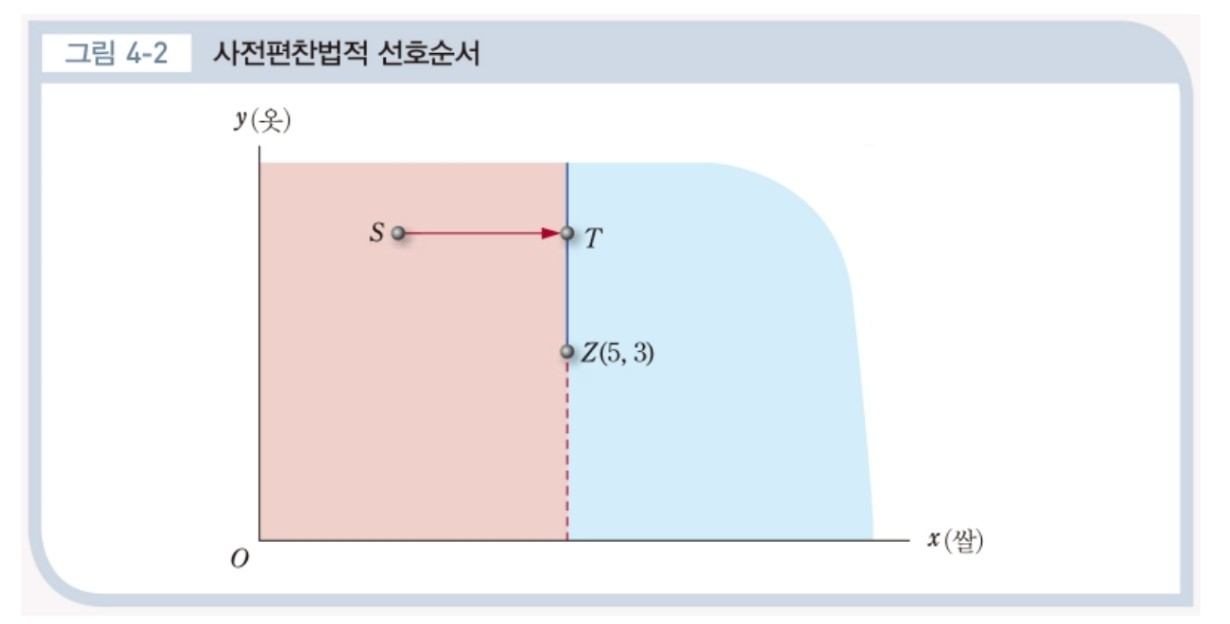
위 그림은 쌀과 옷 사이의 선호관계를 나타냅니다.
소비자는 쌀을 먼저 비교하고 난 뒤에 옷의 양을 따지는 경우인데요(옷보다 쌀을 절대적으로 선호한다),
이러한 경우 소비자는 (쌀 3단위, 옷 100단위)보다 (쌀 4단위, 옷 1단위)를 더 선호하는 극단적인 선호체계를 보이게 됩니다.
이제 S에서 T로 이동하는 경우를 살펴봅시다
S에서 조금씩 오른쪽으로 이동해도 여전히 Z보다 명백히 덜 선호하는 상태가 이어집니다.
쌀의 단위가 Z에서의 쌀의 단위보다 적기 때문이죠.
S가 T점에 거의 근접하게 접근했을 때도 여전히 Z보다 덜 선호됩니다.
하지만 T에 도달하는 순간, 소비자의 선호체계는 갑자기 바뀌게 되는데요,
Z점과 아무런 차이가 없는 상태는 건너뛰어 버리고 갑자기 덜 선호되다가 더 선호되는 상태로 변화한 것입니다.
(연속적이었다면 상품묶음이 조금씩 변함에 따라
명백히 덜 선호 -> 덜 선호 -> 조금 덜 선호 -> 동등 -> 조금 더 선호 -> 더 선호 .....
처럼 변했을 것이지만 이 경우에는 '명백히 덜 선호'에서 '명백히 더 선호'로 갑자기 뛰어버렸죠)
이러한 경우는 연속성 공리가 충족되지 못한 대표적인 경우입니다.
2-4. 강단조성(strong monotonicity)
더 많으면 더 좋다는 뜻
(간단하죠?)
위에서 소개한 공리들이 충족되어야 '연속적인 효용함수'를 상정할 수 있습니다.
다음 시간에는 효용함수와 무차별곡선에 대해 공부해 봅시다!
지금까지 길동이 사촌형이었습니다
슉슉
'길동이의 미시경제학' 카테고리의 다른 글
| <길동이의 미시경제학> 6-2. 한계대체율과 무차별곡선 (12) | 2024.02.14 |
|---|---|
| <길동이의 미시경제학> 6-1. 효용함수와 무차별곡선 (22) | 2024.02.08 |
| <길동이의 미시경제학> 4. 시장의 균형 (균형가격, 정적 안정성, 동적 안정성, 왈라스적 안정성, 마셜적 안정성, 거미집모형, 가격규제) (5) | 2024.02.07 |
| <길동이의 미시경제학> 3. 시장과 수요 공급 (수요함수, 수요곡선, 수요의 가격탄력성, 공급함수, 공급곡선, 공급의 가격탄력성) (2) | 2024.02.06 |
| <길동이의 미시경제학> 2. 미시경제학의 성격 (28) | 2024.02.06 |



